The longest problem

Posted:
Sat Feb 06, 2010 10:39 pmby Cornel
The longest problem (8x8 board):
Cornel Pacurar
9776 feenschach, 2008
(
Dedicated to Itamar Faybish)
Position A:
ser-A=>B in 43743 moves
Special board (with barriers)
Anticirce, PWC, White Minimummer

= Non-capturing Queen
Position B: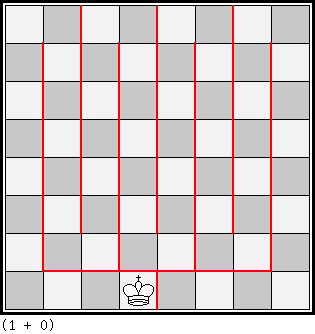
The solution will only be posted here after it appears in feenschach!
The solution is related to the tetrahedral numbers (Ten = 1/6n(n+1)(n+2)). These numbers correspond to placing discrete points in the configuration of a tetrahedron (triangular base pyramid). Tetrahedral numbers are pyramidal numbers with r=3, and are the sum of consecutive triangular numbers. The first few are 1, 4, 10, 20, 35, 56, 84, 120 etc.The number of moves needed to eliminate each of the Black pieces are in fact those triangular numbers (1, 3, 6, 10, 15 etc), and the total number of moves of the solution is the sum of the 63rd tetrahedral number (43680) and the number of consecutive triangular numbers used (63)!
The previous record was 32551.5 moves: Jean-Michel Trillon (dedicated to J. Rotenberg), Rex Multiplex 1982, Special Prize, (Retour à la position du diagramme en 32551.5 coups (3+58))
Re: The longest problem

Posted:
Wed Oct 20, 2010 11:37 pmby apfde
Hello,
here is an idea how to increase the number of moves by 1: Place the white king in the initial position to f1!
Cornel Pacurar (dedicated to Itamar Faybish, 9776 "feenschach" 172, 05-06/2008)
Version
Alfred Pfeiffer, Chemnitz
Position A (left diagram) to Position B (right diagram) in 43744 series moves.

 ser-A=>B in 43744 moves
ser-A=>B in 43744 moves
Grid Chess (special grid), Anticirce type Calvet, PWC, White Minimummer
 = Non-capturing Queen
= Non-capturing Queen1.K*e1[+bQf1] and we reached the former position of Cornel Pacurar
Alfred Pfeiffer
Re: The longest problem

Posted:
Thu Oct 21, 2010 3:46 pmby Cornel
Alfred, I have the following comments related to your post:
1. Interesting usage of the grid - I have not used Grid Chess with special grid, but a special board (with barriers). At first glance, it does seem to solve in the specified number of moves.
2. I was very well aware of the fact that, with my position, an extra move can be added by starting with wKf1, but I preferred my published version. The length record aspect was just one of the two chief elements taken into consideration, the other one was the mathematical representation of the solution. "The solution is related to the tetrahedral numbers (T{n}=1/6n(n+1)(n+2)). The number of moves needed to eliminate each of the Black pieces are in fact those triangular numbers (1, 3, 6, 10, 15 etc.), and the total numbers of moves of the solution is the sum of the 63rd tetrahedral number (43680) and the number of consecutive triangular numbers used (63)!" (See PDB P1109101). By adding the extra move, the above is no longer true and I simply did not want to do that. I still feel the same today.
3. An original posted in the public area of the forum is considered published. If you want to post problems for further discussions and analysis, please post them in the private areas of the forum.
4. In any case, if in the future you make only minor (but valid) improvements to some move-length records (even if more than 0.002286%) , please note that it would be more appropriate to publish them as "[Original Author], version by AP], "instead of AP, after [Original Author]".
Re: The longest problem

Posted:
Thu Oct 21, 2010 4:52 pmby Tungler
Thanks to Cornel for these interesting explanations and also for the good reminders under point 3 and 4. If you have access to the private part of the forum you may sometimes forget that there is also an open part and here really usually published means published! Just as a question to Cornel - maybe that should be somehow be reminded i.e. if you post a diagram - popping up a warning may be helpful...
And to point 4 - the very best in my mind is to write a private message to the author and discuss this with him first before posting. Then such points can already be clarified in advance.

 = Non-capturing Queen
= Non-capturing Queen